This scenario is not unlike putting a drop of dye into a glass of water. The infinite plain is the water, and the dye is the drunks. What will happen as time passes? Obviously, the dye will diffuse into the water (the drunks will scatter randomly across the plain), but how will the dye diffuse, and can we predict it at all mathematically?
To make things simpler, we'll make our drunks one-dimensional. The bar is located at the origin of a line.

Now, you can see (hopefully) that the drunks are free to wander up or down the line. When they fall down, they have an equal chance of heading in either direction.
I'm deliberately setting this up in the same way Einstein did, but without all the math. In his discussion, the drunks were particles, and he set up functions that defined how far they moved and how often, etc.
The drunks (dye) are totally concentrated at the origin. So if you were to graph the concentration of drunks as a function of space, the graph would be 0 everywhere but the origin. At the origin you would have a spike, representing all the drunks.

You could say this is a graph of the function c(x,t) concentration a function of space and time. This graph is c(x,0), all space at time t=0.
We know that as the drunks wander, they will leave the bar (the origin) and slowly spread across the infinitely vast plain. But we want to come up with a mathematical representation of their movements. Can we be precise? The answer is "yes", which probably won't surprise you.
How can we describe the concentration of drunks as a function of both space and time? First, we need to introduce the concept of flow. Flow is the rate of passage of drunks through a point at a certain time. Picture a square placed over our line, so that the line passes through the center, perpendicular to the square.

If three drunks move through the square heading to the right, then the flow at that point at that time is 3. If three drunks move through the square to the right and four drunks move through it to the left, then the flow at that time and position is -1. As a function, flow is:

Now we need to relate "flow" with "concentration". This is actually pretty easy to do. Suppose we have 6 drunks on the left side of the square and 2 on the right.

Once we release them, they're going to spread randomly. So some will move through the square heading right, some will go through the square heading left.

First, the change in concentration with respect to x. We see that there are more on the left than the right, so concentration is decreasing as x is increasing.

The funky symbols in front of 'c' and 'x' are Greek lower case deltas, they represent change. In this case, the change in concentration as x changes.
What about flow? The drunks are moving randomly, so half will go one way and half the other. Three will move through the square heading right, one will go through it heading left. So flow overall is:

And we see that flow is proportional to the negative of the derivative of concentration. Say what? When concentration decreases as you head to the right, that means that flow will be to the right. This jibes with our qualitative understanding of diffusion. There are fewer particles on the right, and we know that particles will diffuse from where they are to where they aren't. Nice.
However, we can't work, mathematically, with that proportionality. Let's get rid of it and stick a nice, fat, "equals" sign in there.
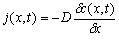
This equation tells us that flow is equal to the negative of the derivative of concentration multiplied by some constant number "D". Hoodoggy. We had to stick that "D" in there because that's what you do when you change from proportionality to equality. You can think of "D" as a factor that transforms one number (change in concentration) to another (flow).
However, this hasn't given us an actual equation. It just relates two functions, both undefined. Can we get rid of flow? (I know, I introduce flow, and now I want to get rid of it? That's what you do in this kind of thing.)
Let's relate flow to concentration in a different way. Instead of a square on the line, let's stick a cube on there.
Now we'll talk about flow and relate it to concentration inside the cube. First, let's state that flow is positive (j>0), that particles are moving to the right.
Posit that at some time t, there are three drunks moving through the square at x = -1, and five drunks moving through the square at x = 1. This corresponds to positive flow and to the case that the flow increases as x increases. In this case, the concentration inside the cube is going to decrease by two drunks.

See that? Three move in, five move out. Now for the functions.

Flow is increasing with x, and concentration is decreasing with time.
Now let's reverse the situation. Now five move in and three move out.

Five move in, three move out, flow is still to the right, it's decreasing, and concentration is increasing.

So now we can generalize this to an equality, right? Hooray! Yes!
 Let's call this Equation 1.
Let's call this Equation 1.Ooh! But we knew from before that
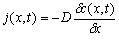
So now we just have to do the math!

And now we can plug this back into Equation 1...

Sweet! We've completely eliminated flow from the picture, and now we have a formula that discusses concentration and ONLY concentration. Booyah! Hmm... But how much information does this equation contain? It's got all those derivatives and that proportionality constant. Fortunately, a member of the sprawling Bernoulli family dealt with situations like this and he's told us how to solve it (Yeah, there were a bunch of mathematical geniuses in one family. Their dinner discussions must've been abstruse awesomeness.)
To deal with this, you have to make a number of assumptions. The first is that:
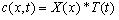
This assumption tells us that concentration is a function of space and time, and that they are independent. This is an assumption that holds true for stochastic motion (random, Brownian, diffusive). It obviously wouldn't hold true for directed motion; throw the ball, and it's path in time and space are fixed and related to each other.
Now we need to plug that back into our big, ugly, derivative-filled equation.

The apostrophes are another notation for derivative that you can use for functions that only have one variable. It saves some space, makes things a bit easier on the eyes.
Now let's rearrange that bad boy so that we get time on one side and space on the other (this is called separation of variables).
 equation 2
equation 2Now that is pretty. And it has the nice property that it can only be true if both sides are equal to a constant (because they involve different variables, see?). This next part is going to have a LOT of equations.
Now we're going to go ahead and assume that T(t) and X(x) are exponential functions, because exponential functions have a nice property. The derivative of an exponential is equal to a constant multiplied by that same exponential (so X'/X is equal to that constant).
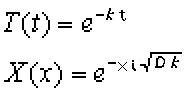
The "k" in each of these is another constant. The "i" in the second formula is a special mathematical constant. It's the square root of -1. Look back to when you learned about square roots and you'll recall you can only take the square root of a positive number. "i" let's you work around that. It's the imaginary number. Cool, eh?
Now we need to check that these fit the requirements of equation 2.

Excellent! The functions we have are a nice little model for the mathematical definition of concentration! If we plug these back in to the definition of c(x,t)=X(x)T(t) and do a little more work, we come up with the pretty result:

"Wait," you say, "where'd all that junk out front come from? Why are 'D' and 't' on the bottom up there? What the holy hell are you doing?" The quick answer: don't fret. It's all just to make sure the function behaves like we want it to. This is really a representation of the probability of finding a particle at a certain location at a certain time. The junk out front makes certain that the probability of finding a particle anywhere at any time is 100%, not more or less than that. The other changes we'll go ahead and illustrate here and now.

Remember, when t=0, at the very beginning of things, we have a spike, with all our drunks inside the bar. Then we hit last call and the drunks start going home. We get a nice little gaussian curve that's still pretty sharp. It's still pretty early, so most of the drunks are still near the bar. However, as time progresses, the drunks get more and more spread out and that curve flattens down. Once we hit infinity, the drunks are evenly distributed across all space and the curve is completely flat. There's an equal probability of finding a drunk at any point.
Now that we've got it in one dimension, want to tack on an additional two dimensions and try doing it again? :shudder: Let's just leave it that this can be expanded to three dimensions without any difficulty.
No comments:
Post a Comment